New gradient theory for thermoelectric structures
Nowadays, great effort is taken on the efficient use and extraction of clean energy from renewable sources to replace the energy from fossil fuels. Thermoelectric materials have the potential to be used to convert waste heat into electricity using the so-called Seebeck’s effect, but their use is hindered by their low efficiency. For the most efficient energy conversion, it is necessary for the material to have the highest possible electrical conductivity and the lowest possible thermal conductivity. With the utilization of various nanotechnologies and nano-composites, it is possible to increase the efficiency of thermoelectric materials. Because the size of the phonon is comparable to nano-sized constructions, it is necessary to consider the size effect. This effect needs to be numerically modeled in order to know the behavior of nano materials in nano structures. Therefore, it is necessary to apply or develop new continuum theories that take this effect into account.
The aim of the presented work on the figure was to create an advanced continuum model for heat transfer in nano structures with consideration of the size effect, using the gradient theory of heat transfer. Constitutive and governing equations for thermoelectric material were derived considering the size effect for heat transfer. An analytical solution was derived for the given boundary value problems and compared with the numerical one. The effect of the size effect was analyzed. Numerical results have shown that the induced potential for a hollow cylinder increases as the thickness of wall of cylinder decreases, i.e. the efficiency of energy conversion increases.
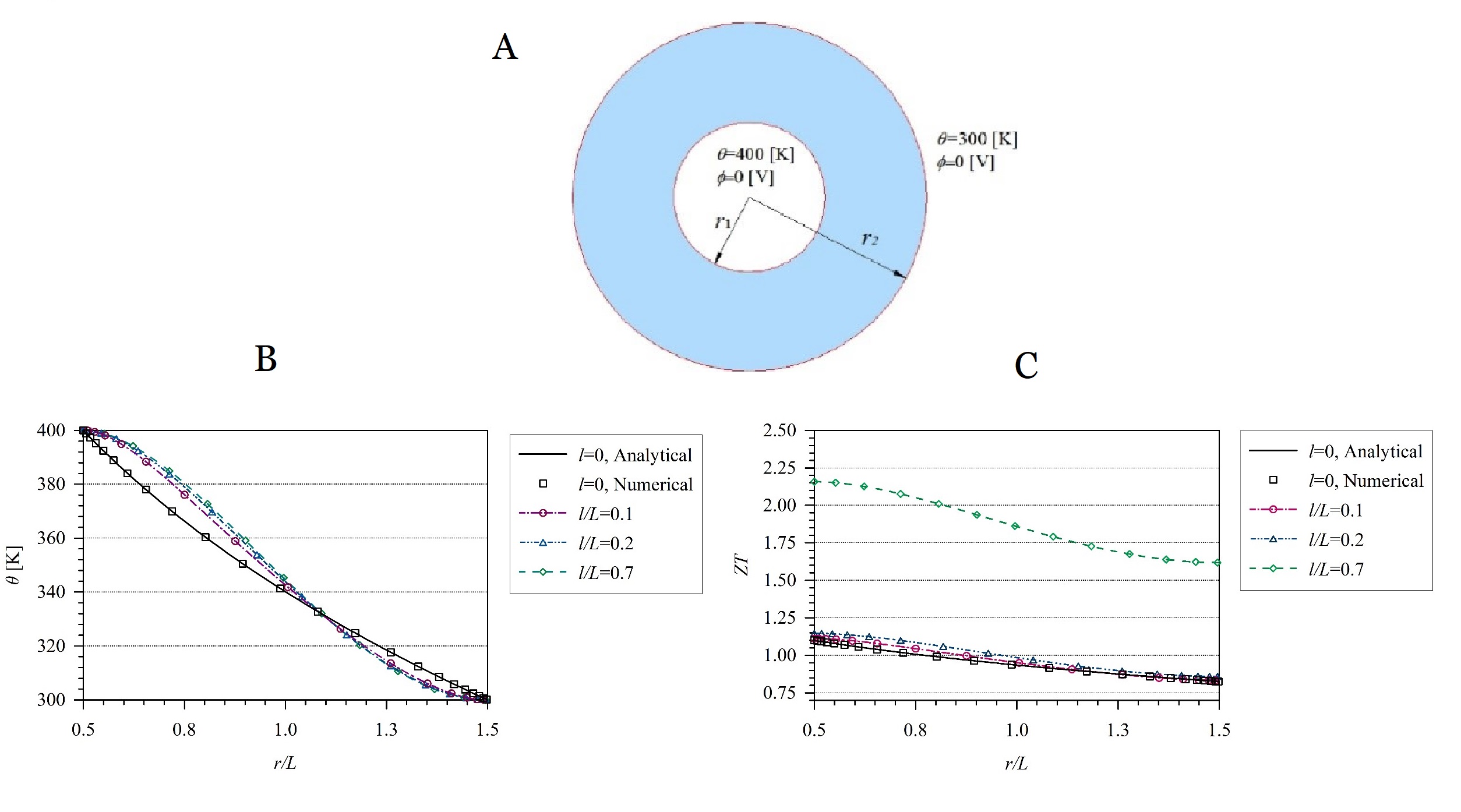
Figure. The geometry and boundary conditions of hollow cylinder (A) and the variation of temperature vs. non-dimensional radius r/L in the hollow cylinder (B) and efficiency of energy conversion (C)

 contact
contact