Numerical modelling of advanced materials within classical and non-classical thermoelasticity

Thermal stresses, especially their discontinuity at the interface between two different materials, often represent a significant damage factor for laminated composite structures. Therefore, there is a need for reliable prediction of thermal stresses in composite structures and it is also a strong motivation to replace laminated plate structures with FGM ones, if it is possible. Therefore, it is a natural effort to solve all these problems using a uniform theoretical basis and the same numerical computational method, which allows to compare the results obtained by different theories with each other but also with other available results. Another current topic in thermoelasticity is the discussion of the velocity of propagation of temperature changes through heat conduction. In classical thermoelasticity, the temperature field is generally bound to the elastic field, but the temperature changes do not propagate with finite velocity like waves. A great effort has been taken into this issue, and today exist various generalized theories of thermoelasticity.
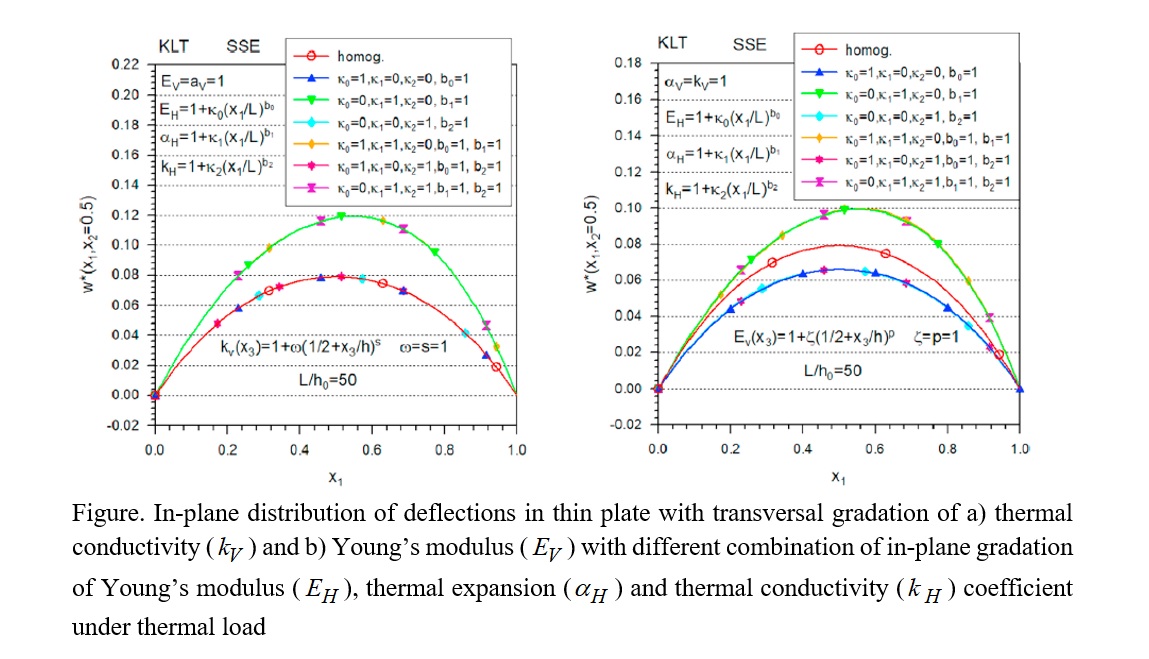
Using the assumptions of classical and non-classical theories of thermoelasticity and plate bending, we have developed a uniform formulation of FGM plate bending, and also a formulation for solving quasi-crystals.