Multiscale modelling of coupled fields in composite materials

The smart composites, where piezoelectric/magneto-electro-elastic fibres are embedded into an elastic matrix can be utilized in advanced structures like sensors or energy harvesting devices. These composites provide superior properties compared to their virgin monolithic constituent materials. Real modelling of piezoelectric or magneto-electro-elastic composite materials requires to consider voids and cracks in these materials. The special theory which consider porosity as a function in constitutive equations has been considered here to smart composites with coupled fields. In the present research project the hybrid/mixed finite element method and the scaled boundary finite element method have been developed to study the effect of porosity on the electromechanical response of piezoelectric materials. Numerical analyses help to enhance the piezoelectric effect in composites. Piezoelectric materials can be characterized as either dielectrics or semiconductors. In semiconductors the induced electric field produces also the electric current. The acoustic-electric effect in piezoelectric semiconductors is the interaction between the mechanical fields and the moving charges. The finite element method is developed to analyse three-dimensional boundary value problems under stationary boundary conditions and with functionally graded material properties in piezoelectric semiconductors. The gradation of material properties can be utilized for optimal design of piezoelectric semiconductor structures. Advances in technology have resulted in the development of small microelectronic components and devices, where classical continuum models cannot be applied due to size effect in micro/nano sized structures. The size-effect is considered by including the strain gradients in advanced continuum models. The size effect reduces the crack opening and J-integral with respect to results obtained by the classical theory.

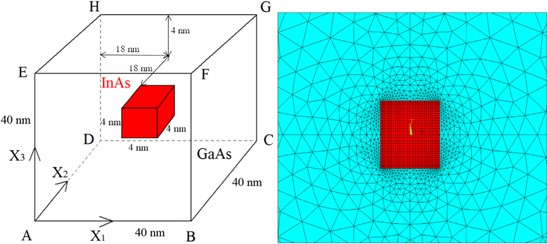
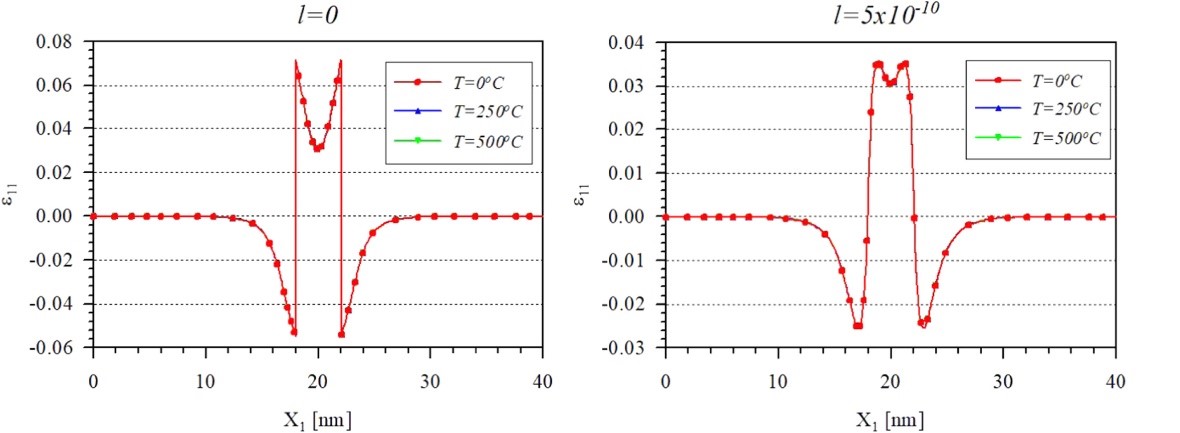
Fig.4. A unit cell of quantum dot structure and cubic dot in a substrate (upper-left) and finite element mesh (upper-right) and the distribution of total normal strain passing QD center at various temperatures with classical elasticity (lower-lesft) and gradient elasticity (lower-right).